目录
1.问题的引入
为什么要降维?
降维的好处
降维的本质
2.降维的主要方法:
2.1 特征选择
2.2 特征抽取
3.主成分分析(PCA)推导
3.1.向量的表示及基变换
3.2.协方差矩阵及优化目标
3.3.算法及实例
3.4.实例
3.5.代码实现
1. 函数原型及参数说明
2. PCA对象的属性
3.PCA常用方法
4.代码示例
1.问题的引入
首先我们应该了解维度或者说维数的概念,在数学维度被定义为独立参数的数目,而在物理学中被定义为独立时空的数目。
例 “点是 0 维、直线是 1 维、平面是 2 维、体是 3 维”
- 点基于点是 0 维:在点上定位一个点,不需要参数
- 点基于直线是 1 维:在直线上定位一个点,需要 1 个参数
- 点基于平面是 2 维:在平面上定位一个点,需要 2 个参数
- 点基于体是 3 维:在体上定位一个点,需要 3 个参数
-
为什么要降维?
- 机器学习中许多算法要求样本满足密采样的条件,但是这个条件在现实任务中通常很难达到,因为即使时一个维数为 20 的数据集,要求满足密采样的条件,至少需要 (103)20=1060(103)20=1060 个样本。现实中的样本属性属性又常常可能高达上百上千,显然这需要的样本数目将是个天文数字。此外很多机器学习方法都涉及到样本之间的距离计算,这在高维的情况下将造成严重的计算困难问题,被称为 “维数灾难”(curse of dimensionality)。
- 在原始的高维空间中,包含冗余信息和噪声信息,会在实际应用中引入误差,影响准确率;而降维可以提取数据内部的本质结构,减少冗余信息和噪声信息造成的误差,提高应用中的精度。
-
降维的好处
- 直观地好处是维度降低了,便于计算和可视化,
- 深层次的意义在于有效信息的提取综合及无用信息的摈弃。
- 虽然人们观测到的是高维数据,但是在数理层面实际学习任务可能只和某个低维分布有关,减少了无效的学习学习过程。
-
降维的本质
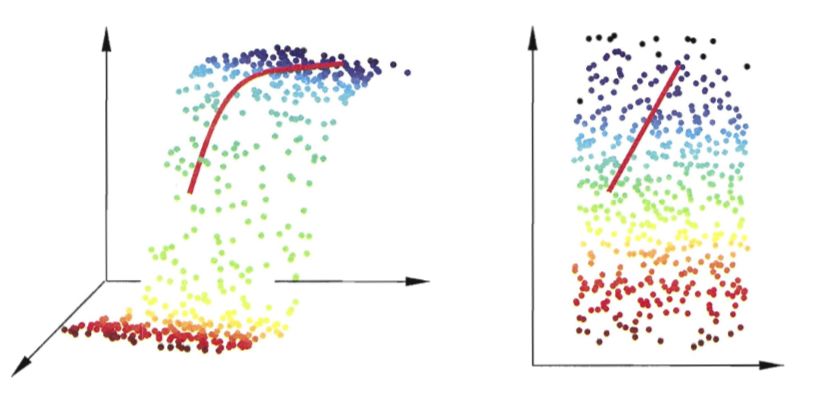
降维的本质实际就是学习一个映射函数f:x→y,其中 x 是原始数据点的表达,目前最多使用向量表达形式。y 是数据点映射后的低维向量表达,通常 y 的维度小于 y 的维度(当然提高维度也是可以的)。f 可能是显式的或隐式的、线性的或非线性的。
2.降维的主要方法:
机器学习中数据降维的方法又很多:
- 主成分分析(Principal Component Analysis)
- 等距映射(Isometric Mapping)
- 局部线性嵌入(Locally Linear Embedding)
- ……
主要可以分为特征选择和特征抽取(特征降维)两类。
2.1 特征选择
特征选择方法是在所有的特征中通过子集搜索算法寻找和模型最相关的特征子集的过程,简单的说就是在所有特征中选择和目标最相关的一些特征,丢弃掉一些不太重要的特征。
特征选择方法又分为三个类型:
- 过滤式
过滤式特征选择方法根据特征的统计学特性选择特征。对于有标签的数据,我们可以计算标签和特征的互信息、相关系数等值,作为特征的得分,然后选择得分比较高的特征。对于没有标签的数据,也可以选择计算特征的方差等值,通常方差较小的特征是无用特征的概率更大一些。经过上述操作,我们就可以简单快速的选择更有用的特征,实现特征降维。
优点: 只需要对特征进行常数级别的遍历,效率高;得到的特征子集使用范围广,后续各种模型都可以使用这个特征子集。
缺点: 特征子集具有冗余性(可以想想为什么,答案在文末);得到的特征子集通常不是最优的。
常用算法:ReliefF、基于互信息的特征选择、基于相关系数的特征选择、基于Fisher-score的特征选择
- 包裹式
包裹式特征选择方法通过训练机器学习模型来选择特征。例如SVM-RFE方法,需要多次调用SVM方法,每次选择表现最好的特征。
优点: 得到的特征子集准确率高;
缺点: 需要多次调用模型,很耗时;得到的特征子集只适用于当前的模型(其他模型使用这个特征子集效果不一定会好)。
常用算法:SVM-RFE
- 嵌入式
在训练机器学习模型的同时选择了特征,例如逻辑回归、LASSO模型。嵌入式特征选择方法的
特点就是在训练好模型的同时,模型会给不同特征不同的权重,使用这个权重来衡量特征的重要性。
优点: 耗时适中,同时有较好的准确率。
缺点: 容易被噪声特征影响。
常用算法:逻辑回归、Lasso
2.2 特征抽取
特征抽取也被称为特征降维,用的最广泛也最常见的一种特征抽取方法就是PCA。特征抽取根据变换的方式分为线性和非线性两种。
- 线性降维
线性降维就是通过某种线性变换,将数据从高维空间映射到低维空间。
举一个简单的例子:比如你在经营一个水果摊子“晴子水果”,好多来你这买水果的顾客都很特
别,每次都会买(3个苹果2个梨)的组合。此时你每次记账都要记:【苹果:3,梨:2】。久而
久之,你决定把3个苹果2个梨组合到一起,称为一个“晴”,之后记账的时候就可以简单记下
【晴:1】。
上述例子有这样的关系:晴1=苹果1/3+梨*1/2,1/3和1/2就是苹果和梨所占的权重。线性降
维就可以理解为寻找高维空间向低维空间映射时每个维度所占的权重,例如PCA就是寻找在低
维空间中数据点的方差尽可能的大,协方差为0时,不同维度所所占的权重。
- 非线性降维
非线性降维指的是是从高维空间向低维空间的转化是非线性的,看下面经典的三维瑞士卷:
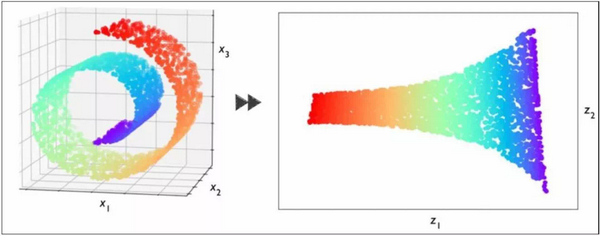
3维瑞士卷数据和利用LE算法得到的二维数据
瑞士卷可以看作是二维数据折叠、弯曲之后展现在三维空间,其本身还是一个二维数据。一种常见的非线性降维思想是认为高维数据在局部上是线性的,我们只需要保证局部线性,就可以将数据从三维转换到二维。以瑞士卷为例,我们可以把瑞士卷看作是很多小块的二维平面在三维空间拼接而成,只要保证这些小的二维平面,就可以将数据从三维空间转化到二维空间。
3.主成分分析(PCA)推导
主成分分析(Principal Component Analysis, PCA)是一种常用的数据分析方法,将原有众多具有一定相关性的指标重新组合成一组少量互相无关的综合指标。
3.1.向量的表示及基变换
PCA的推导过程中涉及大量的线性代数知识,为了能让数理基础不是特别优秀的同学能够彻底理解,那么下面有必要研究一些向量的数学性质。而这些数学性质将成为后续导出PCA的理论基础。
内积与投影
下面先来看一个高中就学过的向量运算:内积。两个维数相同的向量的内积被定义为:
![]()
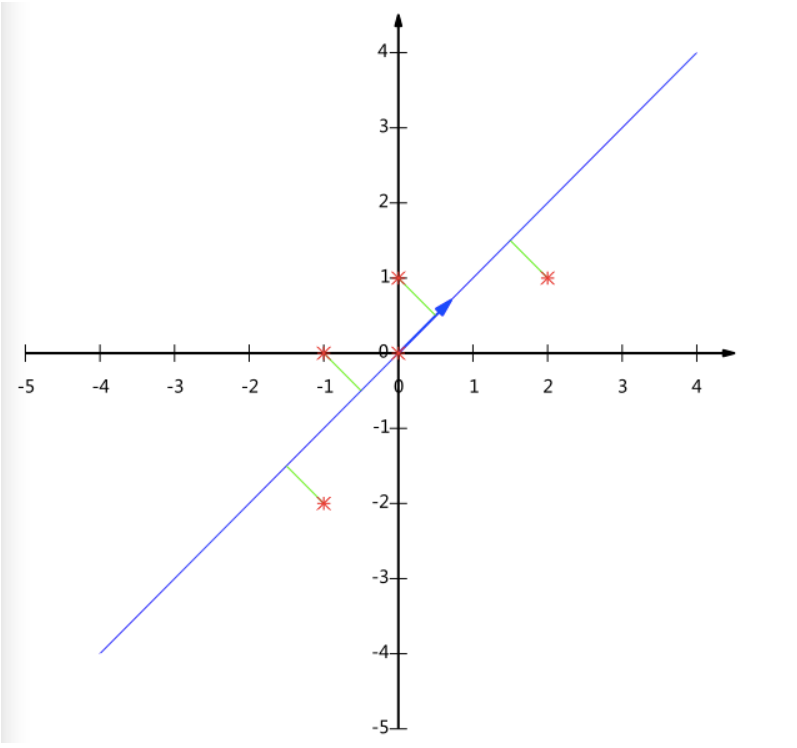
内积运算将两个向量映射为一个实数。其计算方式非常容易理解,但是其意义并不明显。下面我们分析内积的几何意义。假设A和B是两个n维向量,我们知道n维向量可以等价表示为n维空间中的一条从原点发射的有向线段,为了简单起见我们假设A和B均为二维向量,则A=(x1,y1),B=(x2,y2)。则在二维平面上A和B可以用两条发自原点的有向线段表示,见下图:

我们可以看出A到B投影的矢量长度为∣A∣cos(a),其中∣A∣=x12+y12是向量A的模,也就是A线段的标量长度。
到这里还是看不出内积和这东西有什么关系,不过如果我们将内积表示为另一种我们熟悉的形式:
A⋅B=∣A∣∣B∣cos(a)
现在事情似乎是有点眉目了:A与B的内积等于A到B的投影长度乘以B的模。再进一步,如果我们假设B的模为1,即让∣B∣=1,那么就变成了:
A⋅B=∣A∣cos(a)
也就是说,设向量B的模为1,则A与B的内积值等于A向B所在直线投影的矢量长度!这就是内积的一种几何解释,也是我们得到的第一个重要结论。在后面的推导中,将反复使用这个结论。
基
下面我们继续在二维空间内讨论向量。上文说过,一个二维向量可以对应二维笛卡尔直角坐标系中从原点出发的一个有向线段。例如下面这个向量:

在代数表示方面,我们经常用线段终点的点坐标表示向量,例如上面的向量可以表示为(3,2),这是我们再熟悉不过的向量表示。
看起来没有什么问题是吧,似乎任何一个向量都可以通过着这种方式表示。但我们忽略了一个事实,这里的3是指我们在x轴方向上的投影值为3,2是指我们在y轴方向上的投影值为2.也就是说我们默认了以x轴和y轴上正方向长度为1的向量为标准。
更正式的说,向量(x,y)实际上表示线性组合:
x(1,0)T+y(0,1)T
不难证明所有二维向量都可以表示为这样的线性组合。此处(1,0)和(0,1)叫做二维空间中的一组基,更形象的理解我们可以把一组基当作一组坐标系。
所以,要准确描述向量,首先要确定一组基,然后给出在基所在的各个直线上的投影值,就可以了。只不过我们经常省略第一步,而默认以(1,0)和(0,1)为基。
例如,(1,1)和(-1,1)也可以成为一组基。一般来说,我们希望基的模是1,因为从内积的意义可以看到,如果基的模是1,那么就可以方便的用向量点乘基而直接获得其在新基上的坐标了!实际上,这个目标很容易就能实现,我们只要让两个分量分别除以模就好了。例如,上面的基可以变为
![]() 。
。
另外这里要注意的是,我们列举的例子中基是正交的(即内积为0,或直观说相互垂直),但可以成为一组基的唯一要求就是线性无关,非正交的基也是可以的。不过因为正交基有较好的性质,所以一般使用的基都是正交的。
基变换的矩阵表示
一般的,如果我们有M个N维向量,想将其变换为由R个N维向量表示的新空间中,那么首先将R个基按行组成矩阵A,然后将向量按列组成矩阵B,那么两矩阵的乘积AB就是变换结果,其中AB的第m列为A中第m列变换后的结果。
数学表示为:

其中pi是一个行向量,表示第i个基,aj是一个列向量,表示第j个原始数据记录。
特别要注意的是,这里R可以小于N,而R决定了变换后数据的维数。也就是说,我们可以将一N维数据变换到更低维度的空间中去,变换后的维度取决于基的数量。因此这种矩阵相乘的表示也可以表示降维变换。
举个例子:
如果我们有m个二维向量,只要将二维向量按列排成一个两行m列矩阵,然后用“基矩阵”乘以这个矩阵,就得到了所有这些向量在新基下的值。例如(1,1),(2,2),(3,3),想变换到前文(,
),(
,
)那组基上,则可以这样表示:

于是一组向量的基变换被干净的表示为矩阵的相乘。
3.2.协方差矩阵及优化目标
上面我们讨论了选择不同的基可以对同样一组数据给出不同的表示,而且如果基的数量少于向量本身的维数,则可以达到降维的效果。但是我们还没有回答一个最最关键的问题:如何选择基才是最优的?或者说,如果我们有一组N维向量,现在要将其降到K维(K小于N),那么我们应该如何选择K个基才能最大程度保留原有的信息?
要完全数学化这个问题非常繁杂,这里我们用一种非形式化的直观方法来看这个问题。
为了避免过于抽象的讨论,我们仍以一个具体的例子展开。假设我们的数据由五条记录组成,将它们表示成矩阵形式:

其中每一列为一条数据记录,而一行为一个字段。为了后续处理方便,我们首先将每个字段内所有值都减去字段均值,其结果是将每个字段都变为均值为0(这样做的道理和好处后面会看到)。
我们看上面的数据,第一个字段均值为2,第二个字段均值为3,所以变换后:

我们可以看下五条数据在平面直角坐标系内的样子:

现在问题来了:如果我们必须使用一维来表示这些数据,又希望尽量保留原始的信息,你要如何选择?如何选择这个方向(或者说基)才能尽量保留最多的原始信息呢?
一种直观的看法是:希望投影后的投影值尽可能分散。
以上图为例,可以看出如果向x轴投影,那么最左边的两个点会重叠在一起,中间的两个点也会重叠在一起,于是本身四个各不相同的二维点投影后只剩下两个不同的值了,这是一种严重的信息丢失,同理,如果向y轴投影最上面的两个点和分布在x轴上的两个点也会重叠。所以看来x和y轴都不是最好的投影选择。我们直观目测,如果向通过第一象限和第三象限的斜线投影,则五个点在投影后还是可以区分的。
下面,我们用数学方法表述这个问题。
方差
上文说到,我们希望投影后投影值尽可能分散,而这种分散程度,可以用数学上的方差来表述。此处,一个字段的方差可以看做是每个元素与字段均值的差的平方和的均值,即:

由于上面我们已经将每个字段的均值都化为0了,因此方差可以直接用每个元素的平方和除以元素个数表示:

于是上面的问题被形式化表述为:寻找一个一维基,使得所有数据变换为这个基上的坐标表示后,方差值最大。
协方差
对于上面二维降成一维的问题来说,找到那个使得方差最大的方向就可以了。不过对于更高维,还有一个问题需要解决。考虑三维降到二维问题。与之前相同,首先我们希望找到一个方向使得投影后方差最大,这样就完成了第一个方向的选择,继而我们选择第二个投影方向。
如果我们还是单纯只选择方差最大的方向,很明显,这个方向与第一个方向应该是“几乎重合在一起”,显然这样的维度是没有用的,因此,应该有其他约束条件。从直观上说,让两个字段尽可能表示更多的原始信息,我们是不希望它们之间存在(线性)相关性的,因为相关性意味着两个字段不是完全独立,必然存在重复表示的信息。
数学上可以用两个字段的协方差表示其相关性:

由于已经让每个字段均值为0,则:

如果两个变量的变化趋势一致,也就是说如果其中一个大于自身的期望值,另外一个也大于自身的期望值,那么两个变量之间的协方差就是正值。
如果两个变量的变化趋势相反,即其中一个大于自身的期望值,另外一个却小于自身的期望值,那么两个变量之间的协方差就是负值。
当协方差为0时,表示两个字段完全独立。为,我们选择了让协方差为0第二个基时只能在与第一个基正交的方向上选择。因此最终选择的两个方向一定是正交的。
至此,我们得到了降维问题的优化目标:将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段的方差则尽可能大(在正交的约束下,取最大的K个方差)。
协方差矩阵
我们看到,最终要达到的目的与字段内方差及字段间协方差有密切关系。因此我们希望能将两者统一表示,仔细观察发现,两者均可以表示为内积的形式,而内积又与矩阵相乘密切相关。于是我们来了灵感:
假设我们只有a和b两个字段,那么我们将它们按行组成矩阵X:

然后我们用X乘以X的转置,并乘上系数1/m:

奇迹出现了!这个矩阵对角线上的两个元素分别是两个字段的方差,而其它元素是a和b的协方差。两者被统一到了一个矩阵的。
根据矩阵相乘的运算法则,这个结论很容易被推广到一般情况:
设我们有m个n维数据记录,将其按列排成n乘m的矩阵X,设C=m1*X*XT,则C是一个对称矩阵,其对角线分别个各个字段的方差,而第i行j列和j行i列元素相同,表示i和j两个字段的协方差。
协方差矩阵对角化
设原始数据矩阵X对应的协方差矩阵为C,而P是一组基按行组成的矩阵,设Y=PX,则Y为X对P做基变换后的数据。设Y的协方差矩阵为D,我们推导一下D与C的关系:

优化目标变成了寻找一个矩阵P,满足PCPT是一个对角矩阵,并且对角元素按从大到小依次排列,那么P的前K行就是要寻找的基,用P的前K行组成的矩阵乘以X就使得X从N维降到了K维并满足上述优化条件。
由上文知道,协方差矩阵C是一个是对称矩阵,在线性代数上,实对称矩阵有一系列非常好的性质:
1)实对称矩阵不同特征值对应的特征向量必然正交。
2)设特征向量λ重数为r,则必然存在r个线性无关的特征向量对应于λ,因此可以将这r个特征向量单位正交化。
由上面两条可知,一个n行n列的实对称矩阵一定可以找到n个单位正交特征向量,设这n个特征向量为e1,e2,⋯,en,我们将其按列组成矩阵:

则对协方差矩阵C有如下结论:

其中ΛΛ为对角矩阵,其对角元素为各特征向量对应的特征值(可能有重复)。
到这里,我们发现我们已经找到了需要的矩阵P:
![]()
P是协方差矩阵的特征向量单位化后按行排列出的矩阵,其中每一行都是C的一个特征向量。如果设P按照Λ中特征值的从大到小,将特征向量从上到下排列,则用P的前K行组成的矩阵乘以原始数据矩阵X,就得到了我们需要的降维后的数据矩阵Y。
下面我们将给出PCA的一个实例。
3.3.算法及实例
为了巩固上面的理论,我们在这一节给出一个具体的PCA实例。
总结一下PCA的算法步骤:
设有m条n维数据。m*n矩阵
- 将原始数据按列组成n行m列矩阵X
- 将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
- 求出协方差矩阵C=m1XXT
- 求出协方差矩阵的特征值及对应的特征向量
- 将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
- Y=PX即为降维到k维后的数据
3.4.实例
这里以上文提到的

为例,我们用PCA方法将这组二维数据其降到一维。
因为这个矩阵的每行已经是零均值,这里我们直接求协方差矩阵:

然后求其特征值和特征向量,具体求解方法不再详述,可以参考相关资料。求解后特征值为:

其对应的特征向量分别是:

其中对应的特征向量分别是一个通解,�1c1和�2c2可取任意实数。那么标准化后的特征向量为:

因此我们的矩阵P是:

可以验证协方差矩阵C的对角化:

最后我们用P的第一行乘以数据矩阵,就得到了降维后的表示:

降维投影结果如下图:
3.5.代码实现
1. 函数原型及参数说明
这里只挑几个比较重要的参数进行说明。
1sklearn.decomposition.PCA(n_components=None, copy=True, whiten=False)- n_components: int, float, None 或 string,PCA算法中所要保留的主成分个数,也即保留下来的特征个数,如果 n_components = 1,将把原始数据降到一维;如果赋值为string
- n_components ='mle',将自动选取特征个数,使得满足所要求的方差百分比;如果没有赋值,默认为None,特征个数不会改变(特征数据本身会改变)。
- copy:True 或False,默认为True,即是否需要将原始训练数据复制。
- whiten:True 或False,默认为False,即是否白化,使得每个特征具有相同的方差。
2. PCA对象的属性
- explained_variance_ratio_:返回所保留各个特征的方差百分比,如果n_components没有赋值,则所有特征都会返回一个数值且解释方差之和等于1。
- n_components_:返回所保留的特征个数。
3.PCA常用方法
- fit(X): 用数据X来训练PCA模型。
- fit_transform(X):用X来训练PCA模型,同时返回降维后的数据。
- inverse_transform(newData) :将降维后的数据转换成原始数据,但可能不会完全一样,会有些许差别。
- transform(X):将数据X转换成降维后的数据,当模型训练好后,对于新输入的数据,也可以用transform方法来降维。
4.代码示例
| 特征名称 | 描述 |
|---|---|
| sepal length (cm) | 花萼长度(厘米) |
| sepal width (cm) | 花萼宽度(厘米) |
| petal length (cm) | 花瓣长度(厘米) |
| petal width (cm) | 花瓣宽度(厘米) |
5.100000,3.500000,1.400000,0.200000
4.900000,3.000000,1.400000,0.200000
4.700000,3.200000,1.300000,0.200000
4.600000,3.100000,1.500000,0.200000
5.000000,3.600000,1.400000,0.200000
5.400000,3.900000,1.700000,0.400000
4.600000,3.400000,1.400000,0.300000
5.000000,3.400000,1.500000,0.200000
4.400000,2.900000,1.400000,0.200000
4.900000,3.100000,1.500000,0.100000
5.400000,3.700000,1.500000,0.200000
4.800000,3.400000,1.600000,0.200000
4.800000,3.000000,1.400000,0.100000
4.300000,3.000000,1.100000,0.100000
5.800000,4.000000,1.200000,0.200000
5.700000,4.400000,1.500000,0.400000
5.400000,3.900000,1.300000,0.400000
5.100000,3.500000,1.400000,0.300000
5.700000,3.800000,1.700000,0.300000
5.100000,3.800000,1.500000,0.300000
5.400000,3.400000,1.700000,0.200000
5.100000,3.700000,1.500000,0.400000
4.600000,3.600000,1.000000,0.200000
5.100000,3.300000,1.700000,0.500000
4.800000,3.400000,1.900000,0.200000
5.000000,3.000000,1.600000,0.200000
5.000000,3.400000,1.600000,0.400000
5.200000,3.500000,1.500000,0.200000
5.200000,3.400000,1.400000,0.200000
4.700000,3.200000,1.600000,0.200000
4.800000,3.100000,1.600000,0.200000
5.400000,3.400000,1.500000,0.400000
5.200000,4.100000,1.500000,0.100000
5.500000,4.200000,1.400000,0.200000
4.900000,3.100000,1.500000,0.200000
5.000000,3.200000,1.200000,0.200000
5.500000,3.500000,1.300000,0.200000
4.900000,3.600000,1.400000,0.100000
4.400000,3.000000,1.300000,0.200000
5.100000,3.400000,1.500000,0.200000
5.000000,3.500000,1.300000,0.300000
4.500000,2.300000,1.300000,0.300000
4.400000,3.200000,1.300000,0.200000
5.000000,3.500000,1.600000,0.600000
5.100000,3.800000,1.900000,0.400000
4.800000,3.000000,1.400000,0.300000
5.100000,3.800000,1.600000,0.200000
4.600000,3.200000,1.400000,0.200000
5.300000,3.700000,1.500000,0.200000
5.000000,3.300000,1.400000,0.200000
7.000000,3.200000,4.700000,1.400000
6.400000,3.200000,4.500000,1.500000
6.900000,3.100000,4.900000,1.500000
5.500000,2.300000,4.000000,1.300000
6.500000,2.800000,4.600000,1.500000
5.700000,2.800000,4.500000,1.300000
6.300000,3.300000,4.700000,1.600000
4.900000,2.400000,3.300000,1.000000
6.600000,2.900000,4.600000,1.300000
5.200000,2.700000,3.900000,1.400000
5.000000,2.000000,3.500000,1.000000
5.900000,3.000000,4.200000,1.500000
6.000000,2.200000,4.000000,1.000000
6.100000,2.900000,4.700000,1.400000
5.600000,2.900000,3.600000,1.300000
6.700000,3.100000,4.400000,1.400000
5.600000,3.000000,4.500000,1.500000
5.800000,2.700000,4.100000,1.000000
6.200000,2.200000,4.500000,1.500000
5.600000,2.500000,3.900000,1.100000
5.900000,3.200000,4.800000,1.800000
6.100000,2.800000,4.000000,1.300000
6.300000,2.500000,4.900000,1.500000
6.100000,2.800000,4.700000,1.200000
6.400000,2.900000,4.300000,1.300000
6.600000,3.000000,4.400000,1.400000
6.800000,2.800000,4.800000,1.400000
6.700000,3.000000,5.000000,1.700000
6.000000,2.900000,4.500000,1.500000
5.700000,2.600000,3.500000,1.000000
5.500000,2.400000,3.800000,1.100000
5.500000,2.400000,3.700000,1.000000
5.800000,2.700000,3.900000,1.200000
6.000000,2.700000,5.100000,1.600000
5.400000,3.000000,4.500000,1.500000
6.000000,3.400000,4.500000,1.600000
6.700000,3.100000,4.700000,1.500000
6.300000,2.300000,4.400000,1.300000
5.600000,3.000000,4.100000,1.300000
5.500000,2.500000,4.000000,1.300000
5.500000,2.600000,4.400000,1.200000
6.100000,3.000000,4.600000,1.400000
5.800000,2.600000,4.000000,1.200000
5.000000,2.300000,3.300000,1.000000
5.600000,2.700000,4.200000,1.300000
5.700000,3.000000,4.200000,1.200000
5.700000,2.900000,4.200000,1.300000
6.200000,2.900000,4.300000,1.300000
5.100000,2.500000,3.000000,1.100000
5.700000,2.800000,4.100000,1.300000
6.300000,3.300000,6.000000,2.500000
5.800000,2.700000,5.100000,1.900000
7.100000,3.000000,5.900000,2.100000
6.300000,2.900000,5.600000,1.800000
6.500000,3.000000,5.800000,2.200000
7.600000,3.000000,6.600000,2.100000
4.900000,2.500000,4.500000,1.700000
7.300000,2.900000,6.300000,1.800000
6.700000,2.500000,5.800000,1.800000
7.200000,3.600000,6.100000,2.500000
6.500000,3.200000,5.100000,2.000000
6.400000,2.700000,5.300000,1.900000
6.800000,3.000000,5.500000,2.100000
5.700000,2.500000,5.000000,2.000000
5.800000,2.800000,5.100000,2.400000
6.400000,3.200000,5.300000,2.300000
6.500000,3.000000,5.500000,1.800000
7.700000,3.800000,6.700000,2.200000
7.700000,2.600000,6.900000,2.300000
6.000000,2.200000,5.000000,1.500000
6.900000,3.200000,5.700000,2.300000
5.600000,2.800000,4.900000,2.000000
7.700000,2.800000,6.700000,2.000000
6.300000,2.700000,4.900000,1.800000
6.700000,3.300000,5.700000,2.100000
7.200000,3.200000,6.000000,1.800000
6.200000,2.800000,4.800000,1.800000
6.100000,3.000000,4.900000,1.800000
6.400000,2.800000,5.600000,2.100000
7.200000,3.000000,5.800000,1.600000
7.400000,2.800000,6.100000,1.900000
7.900000,3.800000,6.400000,2.000000
6.400000,2.800000,5.600000,2.200000
6.300000,2.800000,5.100000,1.500000
6.100000,2.600000,5.600000,1.400000
7.700000,3.000000,6.100000,2.300000
6.300000,3.400000,5.600000,2.400000
6.400000,3.100000,5.500000,1.800000
6.000000,3.000000,4.800000,1.800000
6.900000,3.100000,5.400000,2.100000
6.700000,3.100000,5.600000,2.400000
6.900000,3.100000,5.100000,2.300000
5.800000,2.700000,5.100000,1.900000
6.800000,3.200000,5.900000,2.300000
6.700000,3.300000,5.700000,2.500000
6.700000,3.000000,5.200000,2.300000
6.300000,2.500000,5.000000,1.900000
6.500000,3.000000,5.200000,2.000000
6.200000,3.400000,5.400000,2.300000
5.900000,3.000000,5.100000,1.800000
from sklearn import datasets # 导入sklearn库中的datasets模块
import matplotlib.pyplot as plt # 导入matplotlib.pyplot模块
import numpy as np # 导入numpy库
from sklearn.decomposition import PCA # 导入PCA类
from pylab import mpl # 导入pylab的mpl
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 设置matplotlib的默认字体为SimHei
mpl.rcParams['axes.unicode_minus'] = False # 设置matplotlib的参数,确保负号正确显示
# 加载鸢尾花数据集
iris = datasets.load_iris()
print(iris) # 打印数据集信息
# 分离特征和标签
X = iris['data'] # 特征
y = iris['target'] # 标签
print('Before pca: \n', X[:5, :]) # 打印降维前的数据
# 初始化PCA对象,指定降维后的维度数为2
pca_1 = PCA(n_components=2)
X_red_1 = pca_1.fit_transform(X) # 执行PCA降维
# 打印降维后的数据
print('After pca: \n', X_red_1[:5, :], '\n')
# 打印每个主成分保留的方差百分比
print('方差百分比: ', pca_1.explained_variance_ratio_)
# 打印当前保留的总方差百分比
print('总方差百分比: ', pca_1.explained_variance_ratio_.sum(), '\n')
# 打印线性变换规则,即主成分
print('components_: \n', pca_1.components_)
# 创建图表
plt.figure(figsize=(6, 6))
# 对每个类别进行散点图绘制
for i in range(2):
plt.scatter(x=X_red_1[np.where(y == i), :][0][:, 0], y=X_red_1[np.where(y == i), :][0][:, 1], alpha=0.8,
label='效果%s' % i)
# 添加图例
plt.legend()
# 显示图表
plt.show()